1) Modifique o exercício 2.9 (sequências de inteiros) para imprimir N inteiros, sendo N um número informado pelo usuário.
2) Utilize while no exercício 2.10 (tabuadas).
3) Modifique o exercício 3.8 (cadastro de aluno) para tratar para, caso o usuário digite valores inválidos no sexo e na nota das provas, o programar informar o erro e solicitar o valor novamente, até que o usuário digite um valor válido.
4) Dada uma coleção de números naturais terminada por 0, imprimir seus quadrados.
5) Dado N, calcular a soma dos N primeiros números naturais.
6) Dado N, imprimir os N primeiros naturais ímpares. Exemplo, para N = 4, a saída deverá ser 1, 3, 5, 7.
7) Durante os 30 dias do mês de abril foram tomadas as temperaturas médias diárias de Euclides da Cunha (BA). Determinar o número de dias desse mês com temperaturas abaixo de zero.
8) Dados x inteiro e n natural, calcular xn.
9) Uma loja de discos anota diariamente durante o mês de março a quantidade de discos vendidos. Determinar em que dia desse mês ocorreu a maior venda e qual foi a quantidade de discos vendida nesse dia.
10) Dados o número N de alunos de uma turma de Programação em C# e suas notas da primeira prova, determinar a maior e a menor nota obtidas por essa turma (nota máxima = 100 e nota mínima = 0).
11) Dados N e uma sequência de N números inteiros, determinar a soma dos números pares.
12) Dado n natural, determinar n!.
13) Dado N e dois números naturais i e j diferentes de 0, imprimir em ordem crescente os N primeiros naturais que são múltiplos de i ou de j ou de ambos. Exemplo, para N = 6, i = 2 e j = 3, a saída deverá ser: 0, 2, 3, 4, 6, 8.
14) Dizemos que um número natural é triangular se ele é produto de três números naturais consecutivos. Exemplo, 120 é triangular, pois 4.5.6 = 120. Dado N natural, verificar se N é triangular.
15) Dizemos que um número natural é primo se ele é divisível apenas por 1 e por ele mesmo. Dado p natural, verificar se p é primo.
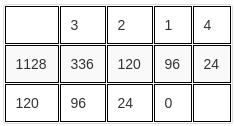
16) Dados dois números inteiros positivos, determinar o máximo divisor comum entre eles usando o algoritmo de Euclides. Exemplo:

O mdc entre 1128 e 336 é 24.
17) Dado N inteiro positivo, dizemos que N é perfeito se for igual à soma de seus divisores positivos diferentes de N.
Exemplo: 6 é perfeito, pois 1 + 2 + 3 = 6.
Verificar se um dado número inteiro positivo é perfeito.
18) Um matemático italiano da Idade Média conseguiu estudar o número de galhos em um certo nível de uma árvore através de uma sequência de números naturais que passou a ser conhecida como sequência de Fibonacci. O n-ésimo número da sequência de Fibonacci Fn é dado pela seguinte fórmula de recorrência:
F1 = 1
F2 = 1
Fi = Fi-1 + Fi-2 para i >= 3.
Faça um programa que dado n calcule Fn.
19) Dizemos que um número i é congruente módulo m a j se i mod m = j mod m.
Exemplo: 35 é congruente módulo 4 a 39, pois 35 mod 4 = 3 = 39 mod 4.
Dados N, j e m naturais não nulos, imprimir os N primeiros naturais congruentes a j módulo m.
20) Dado um número natural na base binária, transformá-lo para a base decimal.
Exemplo, dado 10010 a saída será 18, pois 1.24+0.23+0.22+1.21+0.20 = 18.
21) Dado um número natural na base decimal, transformá-lo para a base binária.
Exemplo, dado 18 a saída deverá ser 10010.
22) Dados três números naturais, verificar se eles formam os lados de um triângulo retângulo.
23) Dados três números, imprimi-los em ordem crescente.
24) Qualquer número natural de quatro algarismos pode ser dividido em duas dezenas formadas pelos seus dois primeiros e dois últimos dígitos.
Exemplos: 1297 (12 e 97) e 5314 (53 e 14).
Escreva um programa que imprima todos os milhares (4 algarismos) cuja raiz quadrada seja a soma das dezenas formadas pela divisão acima.
Exemplo: raiz de 9801 = 99 = 98 + 01. Portanto, 9801 é um dos números a ser impresso.
25) Dados N e uma sequência de N números inteiros, determinar quantos segmentos iguais consecutivos compõem essa sequência.
Exemplo: a sequência 5,2,2,3,4,4,4,4,1,1 é formada por 5 segmentos de números iguais.
26) Dados um inteiro positivo N e uma sequência de N números inteiros, determinar o comprimento de um segmento crescente de comprimento máximo.
Exemplos:
- Na sequência 5,10,3,2,4,7,9,8,5 o comprimento do segmento crescente máximo é 4.
- Na sequência 10,8,7,5,2 o comprimento de um segmento crescente máximo é 1.
27) Simule a execução do programa abaixo destacando a sua saída:
int a, b, total, soma, termo;
a = int.Parse(Console.ReadLine());
b = int.Parse(Console.ReadLine());
Console.WriteLine("({0},{1})", a, b);
total = 0;
soma = 0;
while (a != 0)
{
total++;
termo = 1;
for (int i = 1; i <= b; i++)
termo *= a;
Console.WriteLine("Resp = {0}", termo);
soma += termo;
Console.WriteLine("Soma = {0}", soma);
a = int.Parse(Console.ReadLine());
b = int.Parse(Console.ReadLine());
Console.WriteLine("({0},{1})", a, b);
}
Console.WriteLine("Total de pares = {0}", total);
Console.ReadKey();
Dados:
2 3
5 2
7 1
0 5
3 2